Les débris qui gravitent autour de la Terre évoluent selon une orbite bien définie qui ne se modifie que très rarement... Comment de tels objets ont-ils pu s'affranchir de la gravité terrestre ? Comment ont-ils obtenue cette vitesse et quelle est cette vitesse ? Nous répondrons à ces questions grâce à l'étude de la mise en orbite d'un satellite.

1. Les étapes

A l'heure actuelle, les satellites ne sont pas lancés directement depuis la Terre car on ne sait pas encore leur donner une vitesse initiale suffisante. Le lancement d'un satellite se fait donc grâce à un lanceur de type Ariane 5 afin de lui communiquer une vitesse élevée (détails du fonctionnement d'une fusée ici).

Pour communiquer au satellite une vitesse suffisante à sa satellisation, les fusées comportent généralement plusieurs étages, ce qui permet de se débarrasser, au fur et à mesure de la combustion, d'une masse devenue inutile :

A la fin de ces phases, les derniers étages vont se séparer et le couple lanceur-satellite va petit à petit se placer à l'horizontale montant jusqu'au point d'injection à environ 250 km (c'est-à-dire le point de l'espace où un lanceur libère son satellite en lui communiquant la vitesse suffisante pour décrire l'orbite visée). Arrivé à cette altitude le satellite se sépare de la fusée porteuse.

En effet les lanceurs ne peuvent monter qu'à une centaine de kilomètres. Or certaines orbites sont à des altitudes bien plus élevées : c'est le cas de l'orbite géostationnaire (dite aussi GEO) qui se situe à 36 000 kilomètres. Que se passe t-il donc ensuite ?

Au moment où la fusée va le libérer, la vitesse du satellite est très élevée, si bien qu'il va monter tout seul jusqu'à son orbite :

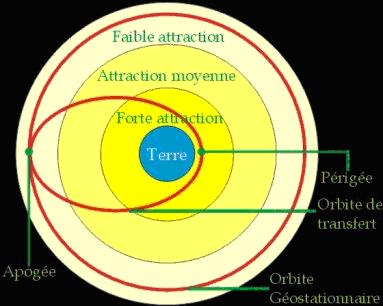
Le satellite s'inscrit tout d'abord dans une orbite dite de transfert qui possèdera une forme elliptique.Son périgée (point le plus proche de la Terre) correspond au point d'injection lanceur/satellite et son apogée (point le plus éloigné) est proche de l'altitude définitive désirée.
Puis, grâce à 3 ou 4 poussées du moteur du satellite, mis à feu lors des passages à l'apogée, l'orbite est progressivement circularisée.

2. La vitesse de satellisation

Le point d'injection se situe généralement entre 170 et 250 km d'altitude. Mais comment avons-nous définie cette altitude ? La réponse à cette question est assez simple :

Bien que cela ne se voie pas, l'air est fait de matière. Les parachutistes plongent dans l'air comme on peut plonger dans l'eau ; sa résistance est beaucoup plus faible mais elle existe. Autour de nous flottent donc d'innombrables molécules dans un espace vide. Ainsi le principal but d'une fusée, ayant pour objet de mettre un satellite en orbite, c'est de le faire s'affranchir du « frein atmosphérique ».
L'atmosphère est divisée en 5 couches ; leurs limites ont été fixées selon des discontinuités dans les variations de la température, en fonction de l'altitude.

	L'exosphère(de 85 à350-800 km d'altitude): c'est la dernière couche de l'atmosphère.
	La thermosphère(de 85 à 350-800 km d'altitude): la température croit avec l'altitude(jusqu'a 1000°). La pression y devient presque nulle et les molécules d'air y sont très rares.
	La mésosphère: la temperature diminue avec l'altitude, de 50 à 85 km
	La stratosphère: la température augmente avec l'altitude jusqu'a 0° (de 6-70 à 70 km d'altitude); elle abrite une bonne partie de la couche d'ozone.
	La troposphère(de la surface du globe à 6-20 km d'altitude). Elle contient 80 à 90% de la masse totale de l'air et la quasi-totalité de la vapeur d'eau. C'est la couche où se produisent les phénomènes metéorologiques.

C'est donc dans la thermosphère que les conditions de satellisation sont optimales ; la vitesse de la fusée y atteint son apogée et le frein atmosphérique n'a pratiquement plus d'effet. La vitesse du satellite ne sera donc que très peu modifiée. Cependant cette vitesse ne doit être ni trop faible (le satellite retomberait sur Terre), ni trop élevée (il s'éloignerait continuellement de la Terre). Elle dépend donc de l'altitude de l'orbite désirée :

3)La vitesse en orbite

Les débris en orbite autour de la Terre ne possèdent donc tous pas la même vitesse. Mais comment les avons-nous calculé ? Au départ, leur vitesse est la même que celle des engins dont ils se sont détachés, c'est-à-dire principalement les satellites qui possèdent une orbite circulaire. Nous allons donc prouver que leur mouvement est uniforme puis ensuite démontrer leur vitesse.

On étudie leur vitesse autour de la Terre, le référentiel est donc géocentrique, de plus les débris proviennent en général d'objet ayant une orbite circulaire autour de notre planète, leur orbite est donc elle aussi circulaire :

D'après la première loi de Kepler (Kepler...mais c'est qui celui-lààà ? ), dans un référentiel héliocentrique, la trajectoire du centre d'une planète est une ellipse dont le centre du Soleil est l'un des foyers. Cette étoile exerce donc sur une planète une force centripète.

D'après la seconde loi de Kepler (Kepler...mais c'est qui celui-lààà ? ), le segment de droite reliant le Soleil à la planète balaie des aires égales pendant des durées égales.

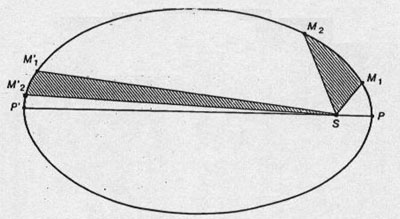
Cependant le mouvement des débris étant circulaire les arcs de cercles balayés sont égaux, le mouvement est donc uniforme :

Lorsque le centre d'inertie d'un solide est animé d'un mouvement circulaire uniforme, en tout point de la trajectoire on a :

Avec a_G l'accélération du solide (en m.s-2).
v_G sa vitesse (en m.s-1).
R le rayon de sa trajectoire (ici altitude de l'orbite du débris + rayon terrestre en mètre m).
Vecteur n le vecteur unitaire centripète .

Ici les débris ne sont influencés que par la force de gravitation centripète notée :

On a donc :

Avec G constante de gravitation de la Terre (en N.m2.kg-2).
M la masse de la Terre (en kg).
m la masse du débris (en kg).

Or d'après la Seconde loi de Newton ( Et c'est qui celui-lààà ? ) ;